고정 헤더 영역
상세 컨텐츠
본문
Greedy Algorithms
미리 정한 기준에 따라 그 때 그 때 가장 최적의 답을 선택하는 알고리즘 -> local optimum
- Coin change
greedy 알고리즘의 활용 -> 최수 수의 동전으로 거스름돈 거슬러주기
예시 ) 74cents = 1(half-dollar)+2(dime)+4(penny)
- Activity-Selection Problem
greedy 알고리즘의 활용 -> 놀이공원에서 가장 많은 놀이기구 탑승하기
activity(놀이기구)들은 각각 시작시간과 종료시간이 다르다. activity들의 정보를 보고 최대 몇개의 활동을 할 수 있을지 구한다.
input : activity(a) 집합의 시작시간 (s), 종료시간(f)

<- 예시이다.
종료시간은 오름차순으로 정렬되어 있다.
활동들을 즐기는 방법은 다양하다.
{a3, a9 a11 }, { a1, a4 a8 a11 } { a2, a4 a9 a11 } 등을 즐길 수 있다. 할 수 있는 최대 활동 수를 선택해야 한다.
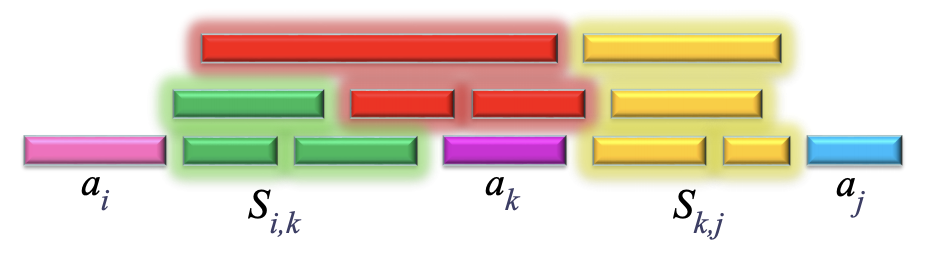
특정활동 ai와 aj가 있을 때, 활동 ai가 끝난 후에 활동이 시작하고 aj가 시작되기 전에 끝나는 활동들의 집합을 Sij라고 한다.
Sij에 들어 있는 상호 양립 가능한 최대 크기의 집합을 찾기를 원하며, 그러한 최대 크기의 집합은 활동 ak를 포함하는 cij라고 가정한다.
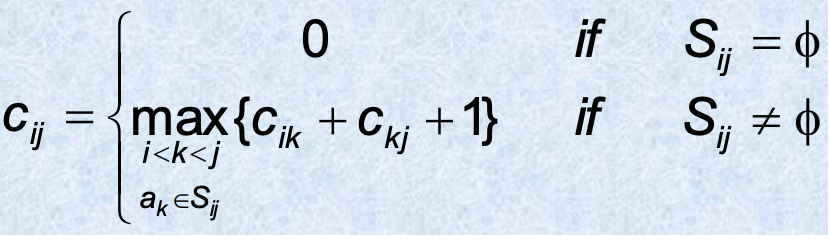
cij에 ak를 포함하면 결국 두 개의 부분 문제가 있는데, 하나는 Sik이고 다른 하나는 Skj이다. 그렇다면, cik=cij ∩ Sik 이고 ckj=cij ∩Skj이다.
cik는 cij에서 ak가 시작하기 전에 끝나는 활동들을 포함하고 ckj는 cij에서 ak가 끝난 후에 시작하는 활동들이 포함된다.
따라서 cij = cik U {ak} U ckj이고,Sij에 들어있는 상호 양립 가능한 활동들의 최대크기 집합 cij는 cik+ckj+1개의 활동들로 이뤄진다.
이 문제는 물론, Dynamic programming 방식으로도 풀 수 있다.

하지만, Dynamic programming 방식은 모든 sub problem을 풀어봐야 한다는 단점이 있다. 필요하지 않은 케이스조차 탐색하는 불필요한 탐색시간을 없애고, 각 단계에서 최적의 선택을 함으로써 효율적인 시간으로 문제를 풀 수 있는 greedy algorithm을 사용한다.
Greedy choice property : 최적의 해결책은 하위 문제에 대한 답을 고려하지 않고 당시 가장 최적의 선택을 함으로써 얻을 수 있다.
- Huffman Codes : Text Encoding
기본 encoding인 ASCII는 모든 알파벳을 7bit로 포함한다.

133bits => 17 bytes
를 필요로 한다.

하지만, 이것도
76bit => 10bytes
를 필요로 한다.
물론, 우리는 12개의 알파벳을 4bit로 표현할 수 있으니 낭비이다
여기에서 가장 좋은 encoding 코드는 호프만 코드 이다. 호프만 코드는 문자열에서 자주 등장하는 문자는 짧은 비트로 표현하고, 거의 등장하지 않는 문자는 긴 비트로 표현한다. (가변 길이 코드)

Huffman code는
65bits => 9bytes
를 필요로 한다.
여기서 주의할 점은 Prefix code여야 한다는 것이다.
Prefix code란 한 코드가 다른 코드의 앞부분이 되지 않는 인코딩 방식 즉, 겹치지 않도록 이진코드를 만드는 것이다.
하프만 알고리즘은 prefix code가 되어야만 decoding 했을 때 문제가 발생하지 않기 때문에 꼭 적용되어야 한다.
예를 들어 non-prefix code로 한다면
a = 01 , m = 10 , n = 111 , o = 0 , r = 11 , s = 1 , t = 0011 이라고 했을 때, 100110111 = 10 0 11 0 111 (moron) = 1 0011 01 11 (star) 어떤 것을 원하는지 혼란이 생기기 때문에 의도하지 않은 방향으로 해석이 될 수도 있다.
Huffman code를 만들기 위해서는 트리를 사용해야 한다.
다음은 알파벳 별 빈도수를 저장한 표와 그를 이용해 하프만 코드 트리를 만든 것이다.


예를 들어, 알파벳 C에 대한 huffman code를 구하는 법을 알아보자면,
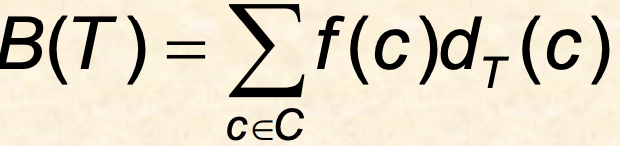
F(c) : c의 빈도수
dT(c) : tree에 있는 C의 leaf의 깊이
B(t) : 파일을 인코딩하는 데 필요한 비트 수
Huffman code의 알고리즘을 보자면,
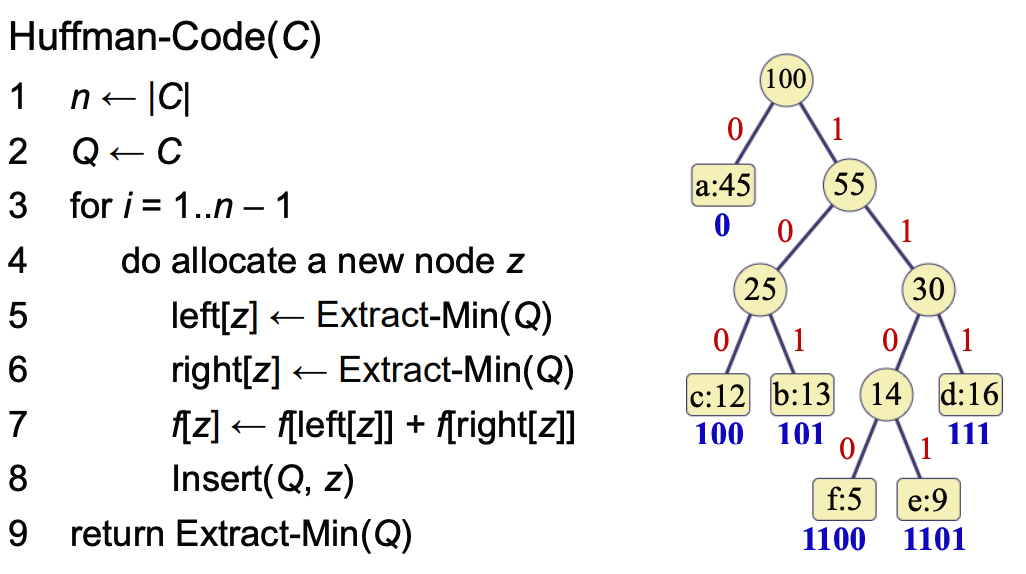
=> Huffman-Code의 Running Time은
O(n lg n) 이다.
'Algorithm' 카테고리의 다른 글
| Shortest path (0) | 2020.05.20 |
|---|---|
| MST _ Prim's Algorithm (0) | 2020.05.17 |
| MST _ Kruskal's algorithm (0) | 2020.05.17 |
| Minimum Spanning Tree (MST) (0) | 2020.05.17 |
| Knapsack Problem (0) | 2020.04.30 |




