고정 헤더 영역
상세 컨텐츠
본문
최단 경로를 찾는 문제의 특징 :
- Input : directed graph G = (V, E) with weight function w : E -> R
- Source에서 Destination까지의 최소 가중치를 가지는 path를 찾는 문제이다.
- p라는 경로의 가중치인 w(p) : p로 가는 길에 있는 모든 edge의 weight의 총합이다.
- u부터 v까지의 shortest-path weight은 다음으로 구한다 :
S(u,v) = 만약 u부터 v까지 가는 path가 존재하면 u에서 v까지는 path인 p 중의 mininum weight
없으면 무한대
- Variants
최단거리를 찾는 문제는 크게 4종류로 나눌 수 있다.
1. Single-source shortest path : 하나의 S에서 모든 vertex까지의 최단거리
2. Sigle -destinations : 모든 vertex에서 하나의 D까지의 최단거리 => direction만 바꾸면 되기 때문에 근본적으로 1번과 같은 원리
3. Single-pair : 하나의 S로부터 모든 하나의 D까지의 최단거리 => single-source shortest path와 풀이방법이 같고 그것보다 빠르게 구할 수 있는 방법이 없어서 사실상 1번과 같다고 본다.
4. All-pairs shortest paths : 모든 vertex의 서로간의 최단거리. S와 D가 여러개이다.
사실상 1~3번은 같은 문제로 보고, Bellman-Ford, DAG, Dijkstara 알고리즘을 이용한다.
4번은 Floyd 알고리즘을 이용한다.
- 문제의 특징
- Optimal substructure가 존재한다. => Dynamic Programming 알고리즘 사용
- Negative Cycle이 절대 존재해서는 안된다. 만약 존재한다면 그 cycle이 계속 돌면서 음의 무한대로 값이 계속 떨어질 것이다.
- Shortest Path란?
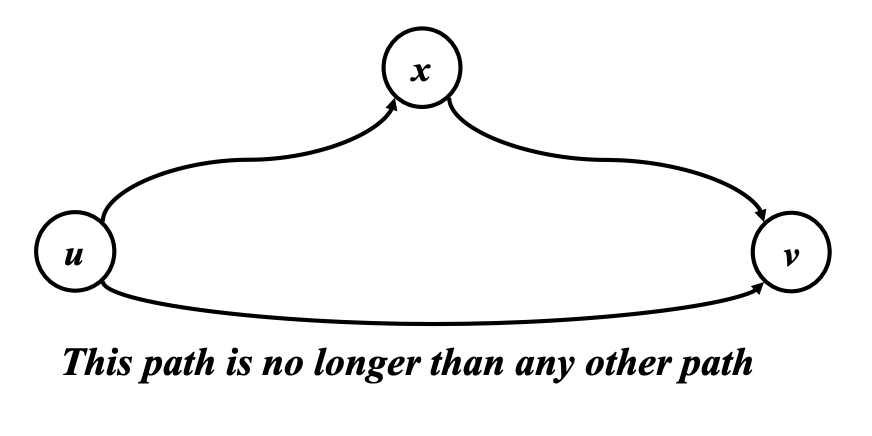
S(u,v) <= S(u,x) + S(x, v) 이다. 즉, 한번 거쳐가는 게 무조건 크거나 같다.
- Shortest path는 Cycle이 없다.
negative-weight cycle : 우리는 negative-weight cycle이 없다고 가정하고 있다.
positive-weight cycle : Shorter path를 갖기 위해서는 그냥 생략함.
zero-weight cycle : 굳이 포함시킬 이유가 없다.
'Algorithm' 카테고리의 다른 글
| All Pairs Shortest Path : Floyd_Warshall Algorithm (0) | 2020.05.20 |
|---|---|
| Single Source Shortest Path (0) | 2020.05.20 |
| MST _ Prim's Algorithm (0) | 2020.05.17 |
| MST _ Kruskal's algorithm (0) | 2020.05.17 |
| Minimum Spanning Tree (MST) (0) | 2020.05.17 |




