All Pairs Shortest Path : Floyd_Warshall Algorithm

ASP는 모든 정점이 출발점이 되어 모든 정점에 대해 최단 경로를 구하는 것이다.

 

가장 쉬운 방법은 Dijkstra 알고리즘 또는 Bellman-Ford 알고리즘을 여러번 돌리는 것이다.

하지만 그렇게 하면, Dijkstra는 O(V^3 ), Bellman-Ford는 O(V^4 )번 걸리기 때문에 빠르지 않다.

그를 위해서 사용하는 더 빠른 알고리즘이 바로 Floyd-Warshall 알고리즘이다.

 

 

 

Floyd-Warshall Algorithm

Dijkstra 알고리즘을 모든 정점에서 수행한 것과 같은 알고리즘이지만 구현이 간단하고 negative-weight edge가 가능하다.

 

- Negative edge를 허용한다 -> 그런 의미에서 Bellman-Ford 알고리즘과 비교한다.

- negative-weight cycle이 없다고 가정한다.

- Dynamic Programming Solution으로 Optimal substructure을 구해서 푼다.

 

 

• DP -최단경로의 구조

두 정점 V1, Vn의 최단경로가 p= <V1, V2, ... , Vn> 일 때, 최단경로의 중간 정점은 p의 양 끝 정점 V1, Vn을 제외한 {V2, V3, ... , Vn-1} 이다.

Floyd-Warshall 알고리즘은 어떤 한 정점이 중간 정점 집합의 한 원소가 되는지 안되는지를 확인하는 것이다.

 

예를 들어, Vi -> Vj 의 최단경로의 중간 정점 집함을 {V1, V2, ... , Vk-1} 라고 할 때, 어떤 새로운 정점 Vk가 중간 정점 집합에 포함되어서 더 비용이 적은 최단 경로를 만드느냐, 아니면 기존의 중간 정점 집합을 유지시키는 것이 최단 경로이느냐를 판단한다.

원래는 하나의 집합인데, Vk가 포함되었다는 것을 표현하기 위해 p1,p2로 나눈 것

 

 

A recursive solution

 

 

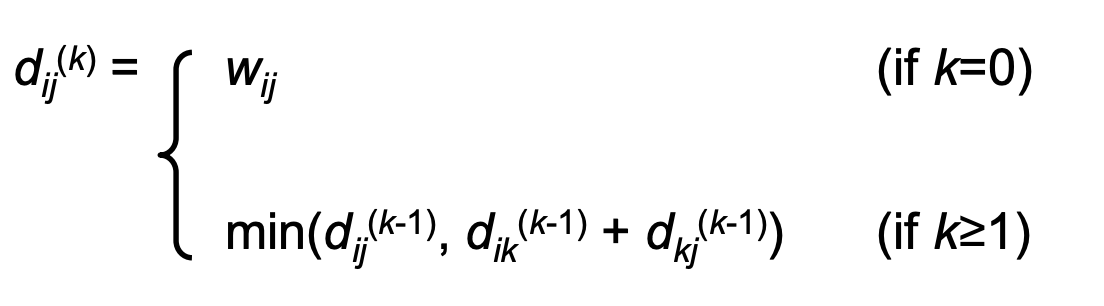
Predecessor pointer에 대한 정보를 담아둔 이차 배열 pred[i, j].

초반에 모든 pred[i,j] = nil 이고, i != j 그리고 wij < ∞ 일 때 pred[i, j] = i 이다.

중간 정점 k를 통과하는 i에서 j까지의 가장 짧은 경로가 발견 될 때마다 pred [i,j]=k로 설정한다.

 

 

 

• 코드

 

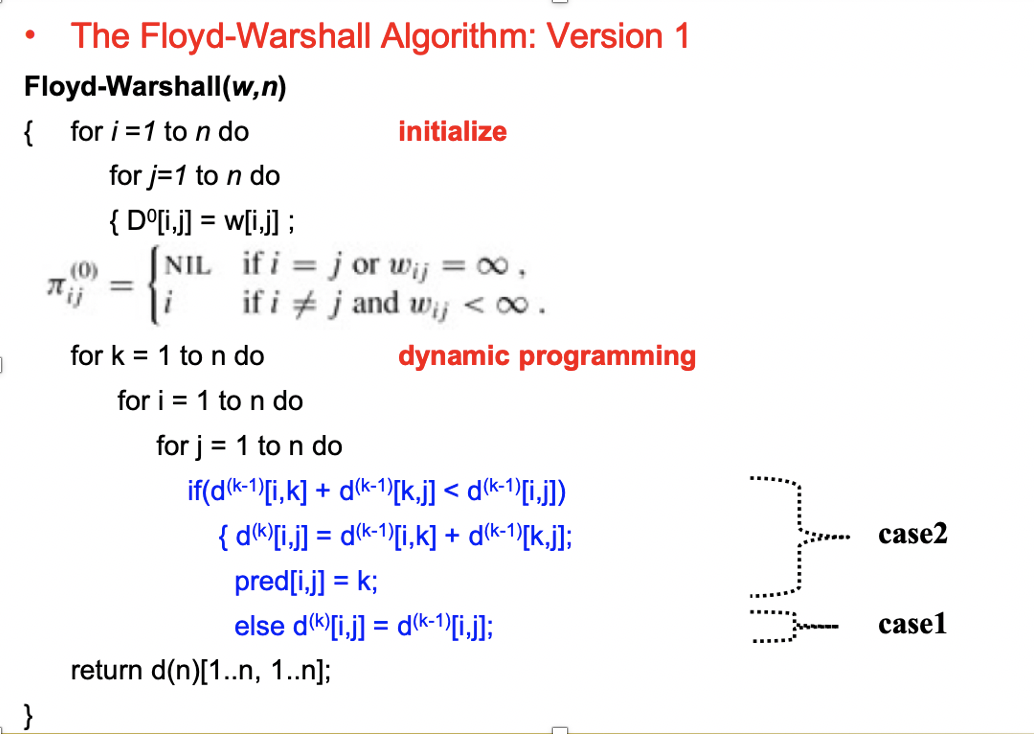
시간 복잡도는 시작 정점 탐색 - 중간 정점 탐색 - 도착 정점 탐색, 이렇게 3개의 for문을 쓰고 있기 때문에 Θ(n^3 ) -> Θ(|V|^3 )  이다.

하지만 공간 복잡도도 Θ(|V|^ 3 ) 이기 때문에 안쓰는거 Initialize해서 바로 그 다음꺼로 사용하는 방법으로 n 대신 하나의 행렬만 유지함으로써 n*n array가 아닌 2*n array를 사용해서 Θ(|V|^ 2 )로 줄일 수 있다. 

 

 

• Example

 

 

 

 

 

• Transitive Closure - Warshall

Transitive Closure란 이 그래프는 원하는 정점이 서로 직접 혹은 간접적으로 연결되어 있냐를 확인할 수 있다.

 

D(k) eotlsdp T(k) = (tij(k))를 사용한다.

 

 

- Transitive Closure 코드

 

 

 

<설명 추가하기>

 

(출처 : https://victorydntmd.tistory.com/108)